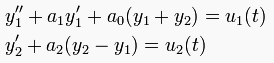I prefer Simulink to Matlab for simulations as doing it with former is much more cleaner and scalable. However some of my trainees prefer Matlab for their own reasons. I wanted to create a how-to post demonstrating this simple procedure.
Simulate the following MIMO system governed by the differential equations
for u1(t) = 0.1sin(t) and u2(t) = 5 (a constant), with initial conditions y1(0) = 1.5 and y2(0) = -0.5 in time range [0,50s]. Given a0=a1=a2 = 1.
I’m unable to put nice latex here, so I’ll define some text notation. A’ in equation above will be written as Adot. A” will be Adotdot. Start with choosing state variables. Obviously, you’ll need at least 3 states, say x1, x2 & x3. Say, x1 = y1, x2 = y1dot & x3 = y2. I hence have
x1dot = x2
x2dot = -a1 x2 - a0(x1+x3) + u1(t)
x3dot = -a2(x3-x1) + u2(t)
y1 = x1
y2 = x3
This is now of the form Xdot = F(X,u(t)) & Y = H(X)
I need to formulate this state equation to be able to write a function to compute F. Create a function file samplesys.m with the following content.
function dx = samplesys(t,x,k)
dx = zeros(3,1);
dx(1) = x(2);
dx(2) = -k(2)*x(2) - k(1)*(x(1)+x(3)) + 0.1*sin(t);
dx(3) = -k(3)*(x(3)-x(1)) + 5;
The system has 3 parameters a0-a1 which I’m passing into the function as a vector k which will have [a0, a1, a2]. Second line with zeros function preallocates memory to make a 3×1 vector for output dx. With n-states this will be an nx1 vector. Once this function is created you can use available ode solvers like ode45 to simulate the system in the following fashion.
>> timeSpan = [0,50]; % Solve from t=0 to t=50
>> IC = [1.5;0;-0.5]; % initial conditions. Note that ic of y1dot (i.e. x2) is not specified, and hence assumed zero.
>> [tsim,y] = ode45(@(t,y,k) samplesys(t,y,[1,1,1]),timeSpan,IC);
That should yield you simulation time ‘tsim’ and output ‘y’ in workspace which can be plotted using plot function. tsim is a column vector with each value specifying simulation time at that time step and y is a matrix with each row giving you states at corresponding time step. Each column of y corresponds to a state chosen.
ode45 uses default max step-size of tspan/50 and rel-tol of 1e-3. If the graph produced is coarse it can be refined with a refine factor (say 20, here) or by lowering max step. These options can be specified using odeset function as
opts = odeset('MaxStep',0.1,'Refine',20);
[tsim,y] = ode45(@(t,y,k) samplesys(t,y,[1,1,1]),timeSpan,IC,opts);
odeset options can optionally be specified at the end of the solver function. Plotting columns 1 & 3 of y w.r.t tsim gives the plots shown. For verification that I coded the function right, I made a simulink model of the same system with same simulation settings and plotted the results against those from Matlab. Unsurprisingly, they overlap.
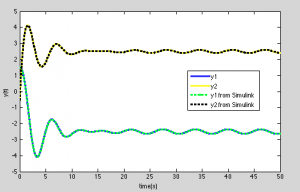
Simulation result & comparison with output of Simulink model
Here I chose to evaluate the inputs u1 & u2 right inside the function. However, they can be inputs to the function too. Function definition in such a case would look like function dx = samplesys(t,x,u1,u2,k). u1 & u2 in such a case must be structures or matrices with time and signal information. Time info is essential as you will have to evaluate u1 & u2 values at the particular instant ‘t’ using interpolation.
ode45 solver has been available in Matlab as a function, but the functions for other solvers like ode15s, ode23, etc haven’t been readily available until recently (R2012b ?). If your version doesn’t have the other solvers try finding them for download on Mathworks support site.
Share your thoughts and tips on using ode functions for our readers.